civil engineering subjects

Tuesday, July 28, 2020

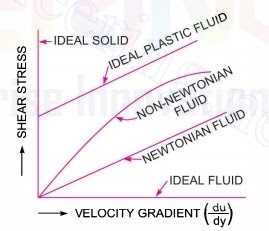
Types of Fluids

ANURAG G TALUKDAR Fluid Mechanics , Newton's law of viscosity

Newtonian fluid,Non-Newtonian fluid, Newton's law of viscosity,Types of Non-Newtonian Fluid,civil engineering jobs,civil engineering subjects

Types of Fluids

The fluids may be classified into the following five types :

l. Ideal fluid
2. Real fluid

3. Newtonian fluid

4. Non-Newtonian fluid and

5. Ideal plastic fluid.

1. Ideal Fluid

A fluid, which is incompressible and is having no viscosity, is known as an ideal fluid. Ideal fluid is only an imaginary fluid as all the fluids which exist have some viscosity.

2. Real Fluid

A fluid, which possesses viscosity, is known as real fluid. All the fluids in actual practice are real fluids.

3. Newtonian Fluid

A real fluid, in which the shear stress is directly proportional to the rate of shear strain is known as a Newtonian fluid. CLICK HERE

4. Non-Newtonian Fluid

A real fluid, in which the shear stress is not proportional to the rate of shear strain (or velocity gradient), known as a Non-Newtonian fluid.

5. Ideal Plastic Fluid

A fluid in which shear stress is more than the yield value and shear stress is proportional to the rate of shear strain (or velocity gradient), is known as ideal plastic fluid.

Newton’s Law of Viscosity

It states that the shear stress (t) on a fluid element layer is directly proportional to the rate of shear strain. The constant of proportionality is called the coefficient of viscosity. Mathematically, it is expressed as

𝜏 = μ du / dy

Fluids which obey the above relation are known as Newtonian fluids and the fluids which do not obey the above relation are called Non-Newtonian fluids.

Non-Newtonian Fluids

Non-Newtonian Fluids are again divided in five types:

i) Dilatant

ii) Pseudo Plastic

iii) Rheopectic

iv) Bingham Plastic

v) Thixotropic

The shear stress for a Non-Newtonian Fluid can be measured by the following formula -

𝜏 = μ (du / dy)^n + B CLICK HERE

i)Dilatant

Here n>1 and B=0 and this type of fluid is also named as shear thickening fluid. eg- sugar in water, quick sand etc.

ii)Pseudo Plastic

Here n<1 and B=0 and this type of fluid is also named as shear thinning fluid. eg- paint, blood, milk etc.

iii)Rheopectic

Here n>1 but B is not equal to zero. eg- gypsum paste, lubricants etc.

iv)Bingham Plastic

Here n=1 but B is not equal to zero. eg- toothpaste, sewage sludge etc.

v)Thixotropic

Here n<1 and B is not equal to zero. eg- ink, ketchup etc.

Viscosity

ANURAG G TALUKDAR Dynamic Viscosity , Fluid Mechanics

Dynamic Viscosity,unit of Viscosity,unit of Dynamic Viscosity, Kinematic Viscosity,unit of Kinematic Viscosity,Fluid Properties,Properties of Fluid,civil engineering subjects,civil engineering jobs

what is Viscosity?

Viscosity is defined as the property of a fluid which offers resistance of the movement of one layer to of fluid over another adjacent layer of the fluid.When two layers of the fluid, a distance 'dy' apart, move one over the other at different velocities, say u and u + du , the Viscosity together with relative velocity causes a shear stress acting between the fluid layers. CLICK HERE

The top layer causes a shear stress on the adjacent lower layer while the lower layer causes a shear stress on the adjacent top layer.This shear stress is proportional to the rate of change of velocity with respect to y.It is denoted by symbol of 𝜏 (Tau).

Mathematically, 𝜏 ∝ du / dy

𝜏 = μ du / dy

where μ (mu) is called co-efficient of Dynamic Viscosity or only viscosity.

Again du / dy = dθ /dt i.e. rate of shear strain or velocity gradient.

The Viscosity is defined as the shear stress required to produce unit rate of shear strain. CLICK HERE

unit of Viscosity

The unit of Viscosity is obtained by putting the dimensions of the quantities in above equation.SI unit of Viscosity is N s/m^2 or Pa.s. Again it can be also expressed in MKS unit as Poise. CLICK HERE

1 N s/m^2 = 10 Poise

Kinematic Viscosity

It is defined as the ratio between the Dynamic Viscosity and Density of fluid.It is denoted by symbol ν (nu). CLICK HERE

Mathematically, ν = μ/ρ

unit of Kinematic Viscosity

By putting on above equation we get SI unit of Kinematic Viscosity is m^2/s.Again as Dynamic Viscosity it can be also expressed in MKS unit in Stokes.

1 cm^2/s = 1 Stokes

CLICK HERE FOR MORE

Specific Gravity

ANURAG G TALUKDAR Fluid Mechanics , Fluid properties

Fluid properties,Properties of fluid, Specific Gravity of water,specific gravity formula,specific gravity definition,specific gravity unit,specific volume,relative density,relative density of water

what is Specific Gravity ?

Specific Gravity is defined as the ratio of the weight density (or density) of a fluid to the weight density (or density) of a standard fluid. For liquids, the standard fluid is taken water and for gases, the standard fluid is taken air. Specific Gravity is also called relative density. CLICK HERE

It is dimensionless quantity and is denoted by symbol S.

Mathematically, S (for liquids) = Density of liquid / Density of water

S (for gases) = Density of gas / Density of air

The weight density of a liquid = S x Weight density of water

= S x 1000 x 9.81 N/m^3

The density of a liquid= S x 1000 kg/m^3 CLICK HERE

If the Specific Gravity of a fluid is known, then the Density of the fluid will be equal to Specific Gravity of fluid multiplied by the density of water. For example, the Specific Gravity of mercury is 13.6 . Hence the Density of mercury = 13.6 x 1000 = 13600 kg/m^3. CLICK HERE

what is Specific Volume ?

Specific volume of a fluid is defined as the volume of a fluid occupied by a unit mass or volume per unit mass of a fluid is called Specific volume. C LICK HERE

Mathematically, Specific Volume = volume of fluid / mass of fluid

= 1 / Density

The Specific volume is the reciprocal of mass density. CLICK HERE

It is expressed as m^3/kg .It is commonly applied to gases.
CLICK HERE FOR MORE

Specific Weight

ANURAG G TALUKDAR Density , Fluid Mechanics

Density, Mass Density, Density of water, Weight Density,Fluid properties, Properties of fluid

what is Specific Weight?

Specific weight or Weight density of a fluid is the ratio between the weight of a fluid to its volume. Thus weight per unit volume of a fluid is called Specific weight and it is denoted by w.

CLICK HERE

Thus mathematically, w = weight of fluid / volume of fluid

= (mass of fluid x acceleration due to gravity) / volume of fluid

= Density x g

Therefore, w = ρ g

The value of Specific Weight or Weight density (w) for water is 9.81 x 1000 N/m^3 in SI units. CLICK HERE

what is Density or Mass Density?

Density or Mass Density of a fluid is defined as the ratio of the mass of a fluid to its volume. Thus mass per unit volume of a fluid is called Density. It is denoted by the symbol of ρ (rho). The unit of Mass Density in SI unit is kg/m^3. CLICK HERE

The Density of liquid may be considered as constant while that of gases changes with the variation of pressure and temperature.

Mathematically, Mass Density is written as

ρ = mass of fluid / volume of fluid

The value of Density of water is 1 gm/cm^3 or 1000 kg/m^3 .

CLICK HERE FOR MORE

CORE OR KERNEL

ANURAG G TALUKDAR core , core is a zone in which stresses are purely

What is CORE OR KERNEL? CLICK HERE

It is the portion of a cross section of a structural member in which nature of stess is same as applied load on the cross section i.e. if applied load is tensile then stress will also be tensile and if it is compressive then stress on the core is also compressive.

Calculation of CORE OR KERNEL: CLICK HERE

A) For circular cross-section

CORE OR KERNEL of a circular cross-section is also circular concentric to the main cross-section.To calculate the area of the core first we have have to calculate the radius of core and it will be maximum eccentricity. CLICK HERE

maximum eccentricity, e = Z/A = d/8

where, d is diameter of the cross-section

Therefore, the area of core = π e ^2 = π d^2/64

Since here e is equal to d/8 therefore e is also called 1/4 th half of the cross-section.

types of kernel,civil engineering subjects

B) For rectangular cross-section

CORE OR KERNEL of a rectangular cross-section is of rhombus shape.Since here Z for both xx and yy axis have different value therefore there will two different e value also.

For x-axis , e(x) = Z(xx)/A = b/6

For y-axis , e(y) = Z(yy)/A = d/6

Thus side of the rhombus , e = sqr root [ e(xx)^2 + e(yy)^2 ]

= 1/3 * [√(b/2)²+(d/2)²]

Therefore, e is called 1/3 rd half of the cross-section.

civil engineering subjects,civil engineering jobs

CLICK HERE FOR MORE

SECTION MODULUS

ANURAG G TALUKDAR Engineering mechanics , Moment of inertia

WHAT IS SECTION MODULUS?

It is a resisting property of cross section of a structural member because of which the member tries to resist the force which causes bending in the member. CLICK HERE

Therefore the safety of the member against bending depends on this parameter and it is directly proportional. That means if section modulus Z increase safety of the member also increase with respect to the members having same cross sectional area but different Z. Therefore we can arrange the following cross sections according to their safety in basis of Z value as :

Stepped section > I section > Rectangular section > Square section > Circular section

section modulus of beam formula,civil engineering subjects,civil engineering jobs

section modulus of beam formula,civil engineering jobs

Calculation of SECTION MODULUS

We can calculate Z with the help of moment of inertia. We have to carefully take the axis of moment of inertia.To calculate Z we have to take the moment of inertia I of that axis which will resist the bending . When in a cross section load is applied along a axis then it is resisted by the other axis perpendicular to it.Therefore,

Z = I(xx)/y or I(yy)/x according to the applied load CLICK HERE

Calculation of MOMENT OF INERTIA

For calculation of moment of inertia we can directly use the formulas for different cross section as mentioned in the following table : CLICK HERE

POLAR SECTION MODULUS

In calculation of Torsional stress we have to consider resistance given by whole cross section since torsion try to rotate the whole cross section and since it varies radially.In this case we have to use a new type of section modulus called POLAR SECTION MODULUS.To calculate this Z we have to take moment of inertia which is summation of both the axis of cross section.Thus,

Z = I/R

where I = I(xx) + I(yy) and

R is the maximum radial distance of given cross section as in figure:

CLICK HERE FOR MORE

LOAD AND EFFECT

ANURAG G TALUKDAR Axial Stress , Bending Stress

WHAT IS LOAD?

Forces acting on a body in its surface is generally called as LOAD. Body forces like gravity,inertia etc. are not included in LOAD.In this blog you will get LOAD AND EFFECT of those loads.

TYPES OF LOAD :CLICK HERE

There are different types of loads based on in which point of the body the load actually applied.These can be classified as-

a) Normal load

b) Shear load

load vs stress,civil engineering subjects,civil engineering jobs

a) Normal load -(P1 and P2)

Loads applied in the direction or parallel to the direction of longitudinal axis is called Normal load.This load can be further classified as-

i) Axial load

ii) Eccentric axial load

b) Shear load -(Q1,Q2,R1 and R2)

Loads applied in the direction or parallel to the direction of any of the transverse axis is called Shear load.This load can be further classified as-

i) Transverse shear load

ii) Eccentric transverse shear load

EFFECTS OF DIFFERENT TYPES OF LOAD :CLICK HERE

i) Axial load -(P1)

Axial load produces Axial stress in structural members acting along longitudinal axis i.e. in z-axis and uniform in every point of y-axis .Therefore we can conclude that axial LOAD AND EFFECT of aixal load is :

Axial stress, σ = P/A (N/mm2)

where, P is the load and A is the area of cross section

ii) Eccentric axial load -(P2)

As shown in fig- the Eccentric axial load can be converted to axial load and a couple and hence it produces axial stress as earlier and bending stress which also acting in the direction of z-axis but in y-axis it is not uniform as shown in fig- .Thus bending stress and axial stress both will act at yz - plane.

Bending stress, σ = M/Z (N/mm2)

where M is constant i.e. M=P.e and

Z is the section modulus and Z= I(xx)/y

CLICK HERE for more about section modulus.

iii) Transverse shear load -(Q1 and R1)

This type of loads produces Shear stress and Variable bending stress in structural member. Shear stress will act on xy - plane and varies along y-axis.Variable bending stress varies in z-direction also since here the bending moment M varies in z-direction according to bending moment diagram (BMD) which you will get in next blog..

The average shear stress is, τ =P/A (N/mm2)

Again, Variable bending stress, σ = M(z)/Z (N/mm2)

where M(z) is the variable bending moment and
Z is the section modulus and Z= I(xx)/y (for Q1 load)

I(yy)/x (for R1 load)

CLICK HERE for more about section modulus.

iv) Eccentric transverse shear load -(Q2 and R2)

This type of load produces shear stress and variable bending stress as earlier and in addition to this it also produces torsional shear stress.Again torsional shear stress will varies in cross section but not in any particular axis.It will vary in radial direction.Therefore we can conclude that Eccentric transverse shear LOAD AND EFFECT of it is as follows:

Torsional shear stress, τ = T/Z(p) (N/mm2)

where T is the torsional moment and T=P.e and
Z(p) is the polar section modulus and Z(p)= I(xx)+I(yy)

CLICK HERE for more about polar section modulus.

In the above fig-05 torsion due to load Q2 is shown and the torsional moment is clockwise in nature.

Tuesday, July 28, 2020

Types of Fluids

1. Ideal Fluid

2. Real Fluid

3. Newtonian Fluid

4. Non-Newtonian Fluid

5. Ideal Plastic Fluid

Newton’s Law of Viscosity

Non-Newtonian Fluids

i)Dilatant

ii)Pseudo Plastic

iii)Rheopectic

iv)Bingham Plastic

v)Thixotropic

what is Viscosity?

unit of Viscosity

Kinematic Viscosity

unit of Kinematic Viscosity

Sunday, July 26, 2020

what is Specific Gravity ?

what is Specific Volume ?

what is Specific Weight?

what is Density or Mass Density?

Saturday, July 25, 2020

What is CORE OR KERNEL? CLICK HERE

Calculation of CORE OR KERNEL: CLICK HERE

A) For circular cross-section

B) For rectangular cross-section

Friday, July 24, 2020

WHAT IS SECTION MODULUS?

Calculation of SECTION MODULUS

Calculation of MOMENT OF INERTIA

POLAR SECTION MODULUS

Thursday, July 23, 2020

WHAT IS LOAD?

TYPES OF LOAD :CLICK HERE

a) Normal load -(P1 and P2)

b) Shear load -(Q1,Q2,R1 and R2)

EFFECTS OF DIFFERENT TYPES OF LOAD :CLICK HERE

i) Axial load -(P1)

ii) Eccentric axial load -(P2)

iii) Transverse shear load -(Q1 and R1)

iv) Eccentric transverse shear load -(Q2 and R2)

About Me CIVIL engineer from NIT silchar,ASSAM(INDIA)

Search This Blog

Most Popular

Recent

Recent Post

Recent Comments